林与鹤

# 思路

把元素从某个位置，变化到另一位置。元素初始化一个随机vector3坐标
定义一个对象，存储想要变化的目标数组，用 tween.js 实现vector3从a位置变化到b位置

 var targets = { table: [], sphere: [], helix: [], grid: [] };

像元素周期表的排列没有规律，所以在 数据组织 中定制
sphere（球体结构），需要用到数学球体坐标系的相关公式推导求得，下面会详细介绍
helix（螺线结构）grid(格子), 也是用到数学方法求得

# 数据组织

//元素，介绍，质量，定制x的位置，定制y的位置
var table = [
  "H", "Hydrogen", "1.00794", 1, 1,
  "He", "Helium", "4.002602", 18, 1,
  "Li", "Lithium", "6.941", 1, 2,
  "Be", "Beryllium", "9.012182", 2, 2,
  "B", "Boron", "10.811", 13, 2,
  "C", "Carbon", "12.0107", 14, 2,
  "N", "Nitrogen", "14.0067", 15, 2,
  "O", "Oxygen", "15.9994", 16, 2,
  "F", "Fluorine", "18.9984032", 17, 2,
  "Ne", "Neon", "20.1797", 18, 2,
  "Na", "Sodium", "22.98976...", 1, 3,
  "Mg", "Magnesium", "24.305", 2, 3,
  "Al", "Aluminium", "26.9815386", 13, 3,
  "Si", "Silicon", "28.0855", 14, 3,
  "P", "Phosphorus", "30.973762", 15, 3,
  ……
];

# THREE.CSS3DObject 初始化dom元素，组织table数组

for ( var i = 0; i < table.length; i += 5 ) {

    var element = document.createElement( 'div' );
    element.className = 'element';
    element.style.backgroundColor = 'rgba(0,127,127,' + ( Math.random() * 0.5 + 0.25 ) + ')';

    var number = document.createElement( 'div' );
    number.className = 'number';
    number.textContent = (i/5) + 1;
    element.appendChild( number );

    var symbol = document.createElement( 'div' );
    symbol.className = 'symbol';
    symbol.textContent = table[ i ];
    element.appendChild( symbol );

    var details = document.createElement( 'div' );
    details.className = 'details';
    details.innerHTML = table[ i + 1 ] + '<br>' + table[ i + 2 ];
    element.appendChild( details );

		//初始化随机位置
    var object = new THREE.CSS3DObject( element );
    object.position.x = Math.random() * 4000 - 2000; //[-2000,4000)
    object.position.y = Math.random() * 4000 - 2000;
    object.position.z = Math.random() * 4000 - 2000;
    scene.add( object );

    objects.push( object );

    //table数组 ---元素周期表的排列

    var object = new THREE.Object3D();
    object.position.x = ( table[ i + 3 ] * 140 ) - 1330;
    object.position.y = - ( table[ i + 4 ] * 180 ) + 990;

    targets.table.push( object );

}

从table数组可以看出，table[ i + 3 ] 和 table[ i + 4 ] 确定了元素周期表中每个元素的 xy坐标，z坐标默认是0。

# sphere数组

sphere坐标的计算用到了一些数学知识。

# 球面坐标

球坐标系是三维坐标系的一种，用以确定三维空间中点、线、面以及体的位置，它以坐标原点为参考点，由方位角、仰角和距离构成。球坐标系在地理学、天文学中都有着广泛应用。

# 定义

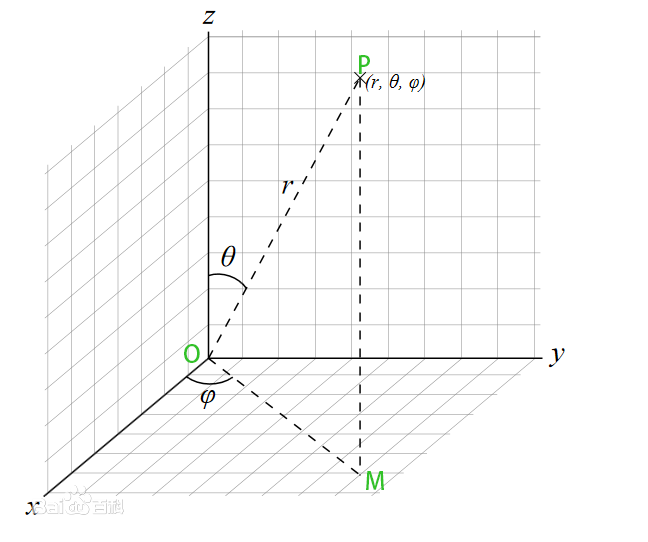
在数学里，球坐标系是一种利用球坐标（r，φ，θ）表示一个点 p 在三维空间的位置的三维正交坐标系。下图显示了球坐标的几何意义：原点与点 P 之间的径向距离 r ，原点到点 P 的连线与正 z-轴之间的天顶角 θ以及原点到点 P 的连线，在 xy-平面的投影线，与正 x-轴之间的方位角 φ 。

# 例解

假设P（x，y，z）为空间内一点，则点P也可用这样三个有次序的数(r，θ，φ)来确定，其中r为原点O与点P间的距离；θ为有向线段OP与z轴正向的夹角；φ为从正z轴来看自x轴按逆时针方向转到OM所转过的角，这里M为点P在xOy面上的投影；。这样的三个数r，θ，φ叫做点P的球面坐标，显然，这里r，θ，φ的变化范围为r∈[0,+∞)，θ∈[0, π]， φ∈[0,2π] ，如图1所示。当r,θ或φ分别为常数时,可以表示如下特殊曲面:r = 常数，即以原点为心的球面；θ= 常数，即以原点为顶点、z轴为轴的圆锥面；φ= 常数，即过z轴的半平面。

# 转换

球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系:

x=rsinθcosφ

y=rsinθsinφ.

z=rcosθ.

反之，直角坐标系(x,y,z)与球坐标系(r,θ,φ)的转换关系为:

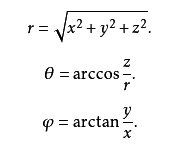
# 代码

var vector = new THREE.Vector3();

for ( var i = 0, l = objects.length; i < l; i ++ ) {
    var phi = Math.acos( -1 + ( 2 * i ) / l ); //[-1，1]反余弦返回0-PI之间的弧度
    var theta = Math.sqrt( l * Math.PI ) * phi; //[0,20PI]

    var object = new THREE.Object3D();
    object.position.x = 800 * Math.cos( theta ) * Math.sin( phi );
    object.position.y = 800 * Math.sin( theta ) * Math.sin( phi );
    object.position.z = 800 * Math.cos( phi );
    vector.copy( object.position ).multiplyScalar( 1 );
    object.lookAt( vector );

    targets.sphere.push( object );
}

r是确定的，所以计算出 phi theta，就能确定球面上的位置。

# helix

 // helix
var vector = new THREE.Vector3();

for ( var i = 0, l = objects.length; i < l; i ++ ) {

  var phi = i * 0.175 + Math.PI;

  var object = new THREE.Object3D();

  object.position.x = 900 * Math.sin( phi );
  object.position.y = - ( i * 8 ) + 450;
  object.position.z = 900 * Math.cos( phi );

  vector.x = object.position.x * 2;
  vector.y = object.position.y;
  vector.z = object.position.z * 2;

  object.lookAt( vector );

  targets.helix.push( object );

}

# grid

// grid
for ( var i = 0; i < objects.length; i ++ ) {

    var object = new THREE.Object3D();

    object.position.x = ( ( i % 5 ) * 400 ) - 800;
    object.position.y = ( - ( Math.floor( i / 5 ) % 5 ) * 400 ) + 800;
    object.position.z = ( Math.floor( i / 25 ) ) * 1000 - 2000;

    targets.grid.push( object );

}

# 变形

//调用：  
transform( targets.sphere, 2000 );

function transform( targets, duration ) {

  TWEEN.removeAll();

  for ( var i = 0; i < objects.length; i ++ ) {

      var object = objects[ i ];
      var target = targets[ i ];

      new TWEEN.Tween( object.position )
          .to( { x: target.position.x, y: target.position.y, z: target.position.z }, Math.random() * duration + duration )
          .easing( TWEEN.Easing.Exponential.InOut )
          .start();

      new TWEEN.Tween( object.rotation )
          .to( { x: target.rotation.x, y: target.rotation.y, z: target.rotation.z }, Math.random() * duration + duration )
          .easing( TWEEN.Easing.Exponential.InOut )
          .start();

  }

  new TWEEN.Tween( this )
      .to( {}, duration * 2 )
      .onUpdate( render )
      .start();

}

# 初始化

camera = new THREE.PerspectiveCamera( 40, window.innerWidth / window.innerHeight, 1, 10000 );
camera.position.z = 3000;
camera.position.y = 0;
scene = new THREE.Scene();

# 渲染及循环

function animate() {

  requestAnimationFrame( animate );

  TWEEN.update();

  controls.update();

}

function render() {

  renderer.render( scene, camera );

}

← 灯光